SFⅡｰ2で、BP曲線は、資本規制係数k＃に依って表される資本規制の程度により、ｋ＝０、ｋ＝∞、ｋ＞０の場合がある旨述べておいたが、k＝∞　⇔　r＝r＊の場合を、テキストによりマンデルｰフレミング・モデルと呼んでいるケースもある。

＃厳密な定義上は、資本移動の自由度とその移動に伴うリスクの程度と捉えるべきものであり、∞も、移動の自由度が完全でありリスクも無視し得る事から、利子に対する所得の弾力性が∞となる、と考えるべきもののようであるが、ここは、”Brilliant Gadget"から、何らかの洞察がえられないか、との観点から検討を加えている事から、資本移動が、政策的経済的に規制される程度、との認識で取り扱っておく。

そこで、r＝r＊、即ち、BP曲線が水平となる場合に、どのような知見が得られるかを、まず、見てみたいと思う。

 

 

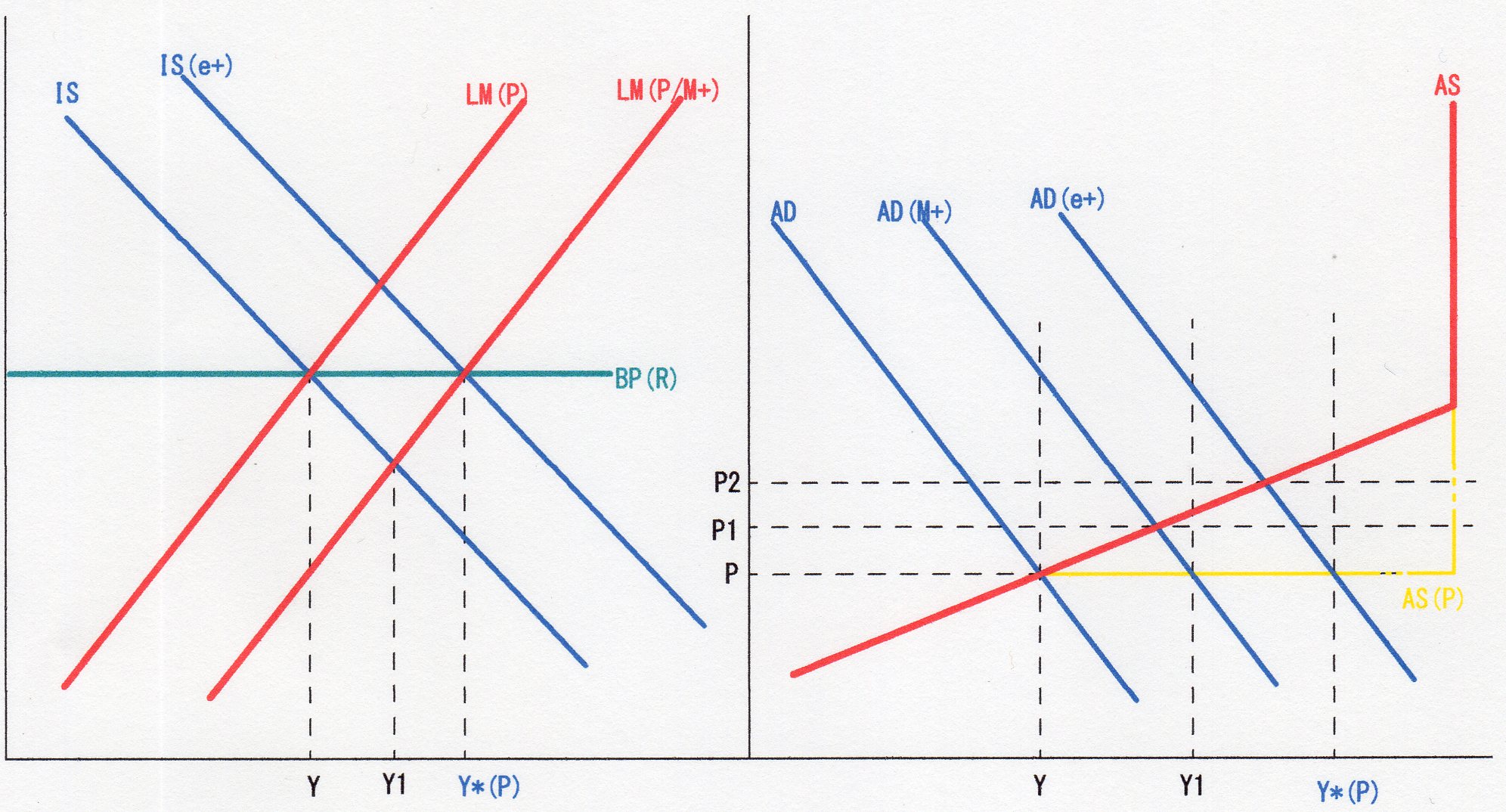
上図左が、（狭義の）マンデルｰフレミング・モデルのBP曲線がｒ＝Rで水平な直線となっているIS-LM-BP分析図である。

今、価格Pの時、R・Yで均衡しているとした場合、Mを増加させるとLM曲線はLM(P/M+)へと右シフトする。そうすると、IS曲線との交点Y1での利率ｒはRより低いために、資金流出→資本収支悪化→国際収支赤字→国際収支バランス改善の要→経常収支改善の要→自国通貨建て外貨価格eの上昇・自国通貨安→eX･輸出の増加→IS曲線の右シフト→Y*(P)・Rでの均衡が果たされる、と通常は解される。

この時、上図右でのAS-AS分析上ではどのような変化が起きているのかを見ると、当初のＲ･Ｙの時、価格はＰとしてあるから、右図ではＰ･Ｙで均衡している。ここから、Ｍの増加によりＡＤ曲線はＡＤ（Ｍ＋）に右シフトする事となり、更にISがe+によりIS(e+)に右シフトする事により、もう一段AD(e+)に右シフトする事になる。

ここで問題となるのは、左のIS-LM-BP分析上のでの所得は、Y→Y1→Y*(P)で推移・均衡していると言うことであり、これらは、右図のAD-AS分析図上では、何れも、価格P上での各AD曲線との交点である。従って、これらを結んだAS曲線はAS(P)で示される水平線であり、右上がりのASではないと言うことである。

この完全雇用に至るまでは価格Pで水平、完全雇用水準以上では垂直となるAS曲線は、「需給の不一致は完全雇用水準達成以降は”価格調整”により為されるが、それ以前は”数量調整”により為される、よって、価格は、完全雇用水準までは一定となる」という”ケインズ”乃至初期ケインズ経済学の45°線分析モデル上のAS曲線であり、AS(P)と各AD曲線の交点であるY・Y1・Y*(P)は、「総需要の水準が国民所得の水準を決定する」という有効需要の原理を表している図となるものである。

とすれば、IS-LM-BP分析上このモデル的制限がどこにあるかとみれば、それは、

　　　　　　　　　LM；M/P=LM(ｒ・Y)

と言うLM式にあり、ここでPはM同様定数であり、外部的に決定・与えられなければ変化しようがないものである。

この点、上図右のAD-AS分析図においては、この価格Pの推移が示し得る事から右上がりASによるIS-LM-BP分析が如何なるものになるかを次に見てみたい。

 

 

 

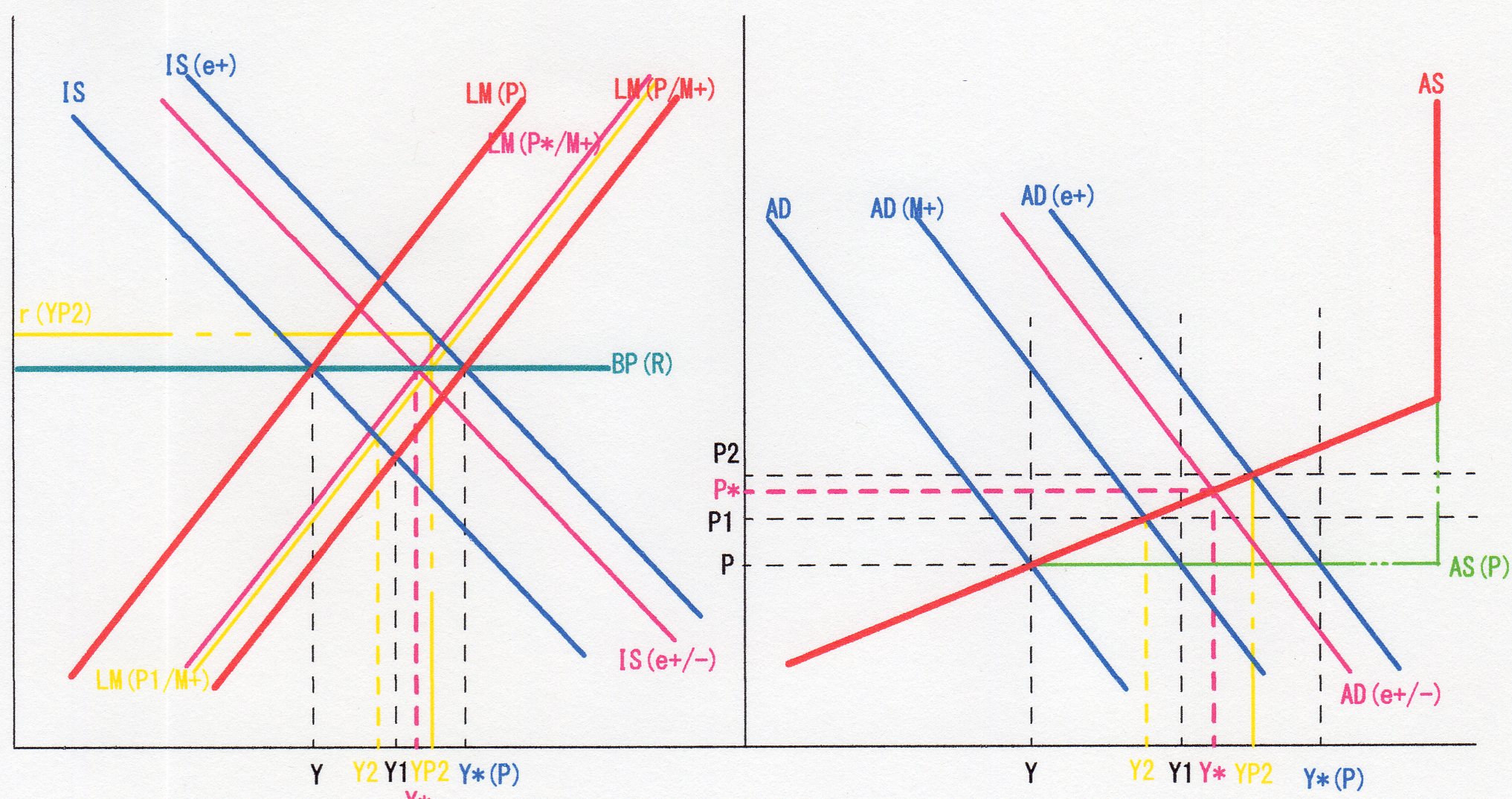
上図の如く、ASによって価格が変化する場合を図示すると相当複雑・見づらくなるが、一見、Pで価格が一定の場合の最終均衡値Y*(P)に対し、価格がP*へと上昇するためにY*は小さくなることが見て取れる。そして、この図は、AD-AS分析上デｲマンドプル・インフレーションを表す図でもある。

まず、LM(P*/M+)に右シフトする事によりAD(M+)に右シフトし、価格PにおいてはY1と成っているが、AS上ではAD(M+)との交点はP1と価格が上昇すると共にY2へ所得が減少する。これは、ASとPとの交点の所得は当初所得のYであり、Y1-Yの需要超過が生じており、”価格調整”により需給の調整が行われる為であり、先の”数量調整”により需給が一致するという”ケインズ”的有効需要の原理と違うケインジアン的AD-AS分析の為である。

従って、r－Y平面上では、LM(P1/M+)へ左方向に逆シフトする事になるが、この時、ISとの交点でのrはRより低いために、件の資金流出→資本勘定悪化→eの上昇→eX・輸出の増加→ISの右シフトとなりIS(e＋）となり、P-Y平面ではAD(e+)へのさらなる右シフトが起きる。

そして、この時、Pとの交点は、Y*(P)であり、p=一定とする”数量調整”による需給調整においては、ここが均衡所得と成ったが、AS上での交点は”価格調整”によりP2並びにY２となる。そして、このY2とIS（e+)との交点での金利r(YP2)は今度は、Rより高くなる。とすると、今度は、資金流入→資本収支の改善→国際収支の黒字化→国際収支のバランス化の為に経常収支の悪化の要→eのe-への下落・自国通貨高の要→eX･輸出減が生じ、IS曲線の左方綱へのキックバック並びにLM曲線のさらなる左シフトが起きることとなり、AD曲線も左方向へキックバックする事になる。

そして、これらのシフトは、BP(R)でIS(e+/-)及びLM(P*/M+)が交わる一方、AD(e+/-)が交点P*・Y*で交わる迄続き、ここが、最終均衡点となる。

では、これらの最終均衡点は保証されうるのか？

それには、各曲線を表す数式を今一度見る必要があり、

　　　　　　　　　　　IS;Y=IS（ｒ・e｜ｃ・G・X・ｍ）

　　　　　　　　　　　LM；M＝LM（ｒ・Y・P )

　　　　　　　　　　　BP;r= BP（e ・Y｜X・ｍ・ｋ・r* ) = R

となり、通常のIS-LM-BP分析においては、LM式において定数とされるPが未知数とされるために、未知数がY・ｒ・e・Pの四つに対し、方程式が三本、ｋ＝∞とする事によりｒ＝Rと定数となるとしても、未知数３・方程式２となり、解は不定となる。

そこで、AD-AS分析において、

　　　　　　　　　　　AD（P・Y・e）＝AS（ P・Y )

が、追加されているために、未知数４に対し方程式4となり、解が一意的に定まる事が担保され得る。

所で、このAD乃至AS式が如何なるものであるかは、まず、AD式は、IS式及びLM式からｒを除去する事により得られる。

　　　　　　　　　　ｒ= IS^ （ e・Y )

　　　　　　　【^は,IS式をｒについて書き換えた意。定数部分は書かない。以下同】

　　　　　　　　　　ｒ = LM^ ( Y・P )

　　　　　　　　∴　IS＾( e・Y ) = LM^ ( Y・P )

　　　　　　　　∴　AD; P = AD ( e・Y )

となっている。(なお、eは,P-Y平面上では、r-Y平面上と同じく、外生変数となる。)

一方、AS曲線については、SF４において、”四連図”においてその導出について、上図水平となるAS曲線も含めて記述してはいたが大分前になるので簡単にお復習いすると、やや小さくて見にくいが、下図のとおり、

 

 

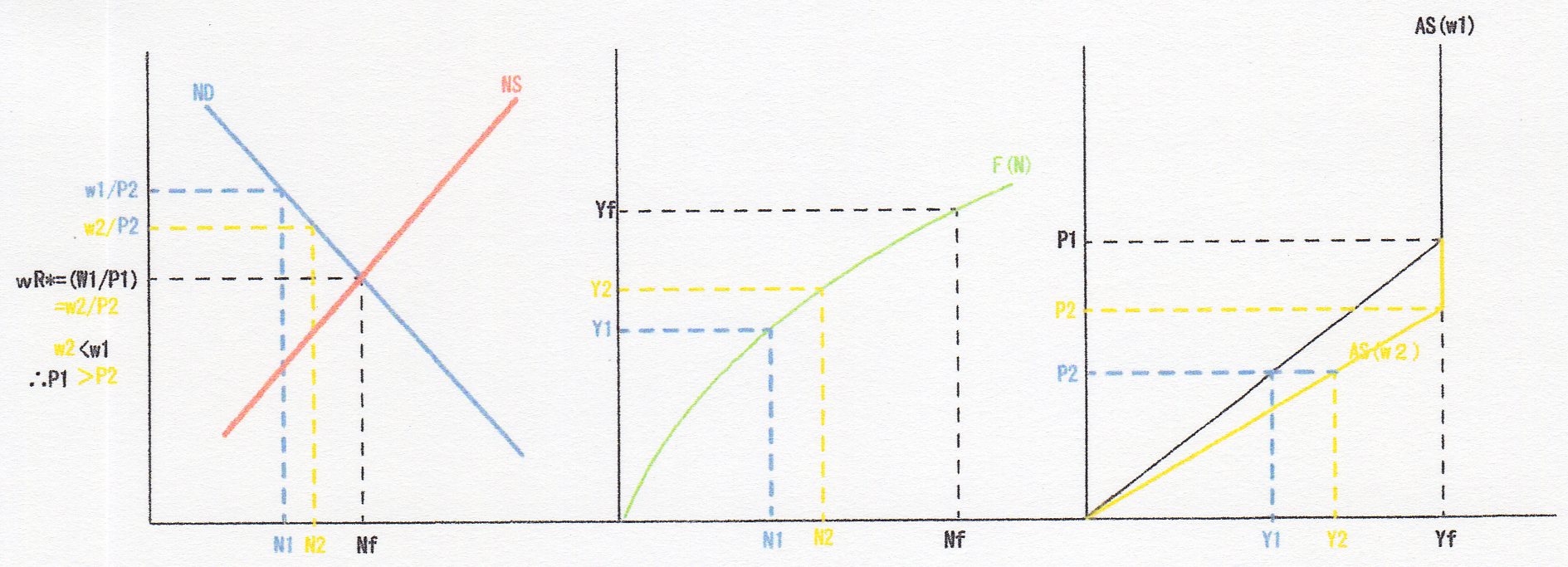
まず、一番右側の図が労働市場均衡を表し、労働需要ND曲線と労働供給NS曲線を表し、実質賃金wRが一致するｗR*に対応する労働需要量Nfが完全雇用水準となる。

次の二番目の図が生産市場を表し、労働投入量Nfに対し、生産関数F(N)により、算出されるYfが完全雇用所得となる。

そして三番目がAS曲線を表す図となり、Yfに対応する価格Pは、名目賃金をw1としてｗR*で除すれば得られるからこれをP1とすれば、P-Y平面上にP1・Yfの交点を得ることが出来、Yfは完全雇用所得であるから、AS曲線はここから垂直となりAS(w１)を得ることが出来る。

ここで、古典派乃至マネタリストはこの名目賃金ｗは価格Pに対して、相対的に可変的、即ち、労働供給NSは実質賃金ｗRの増減に依って連続的に増減すると考えるから、価格Pの増減は相対的名目賃金ｗの増減に依って相殺され、wR*は常に実現する。従って、総供給曲線ASはYfで垂直となる。

しかし、ケインズ乃至ケインジアンは、名目賃金は物価上昇の場合は相対的可変的に上昇するが、物価下落の場合は一定限度以下には下落しない下方硬直的名目賃金ｗを考える。（そして、これは、労働組合の存在等により、検証可能・妥当な仮説とされる）

そこで、ｗ１を下方硬直的賃金w1とすれば、価格PがP2に下落したとき、実質賃金w1/P2はｗR*より高いから労働需要量N1に対し、労働供給量の超過が生じる。この時、更に、賃金の下方硬直性がある場合にはN1で労働力が決定されるとするショートサイド理論によって、労働投入量はN1に決まることになる。

従って、二番目の生産関数に依って、産出量はY1に決定され、AS曲線はP2・Y1を通る右上がりの曲線と成る訳であった。

また、下方硬直的賃金w1がw2に低下したとき、w2/P2はw1/P2より低いためN2で労働投入量は決定され、生産量はY2となる。

この時、ｗR*となる価格をP2とすると、図に示したとおり、w2＜ｗ１であるから、P2<P1となる。

従って、これらを第三番目の図に示せば、P2・Y２を通り、P2でYfとなる右上がりのAS(w2)となり、（下方硬直的名目）賃金の低下によるAS曲線の下方シフトが示し得たことにもなる。

そこで、AS曲線を式で表すには、上の三連図の

　　　　労働市場N；　ND = NS

　　　　生産市場Y；　Y = F ( N )

　　　　AS曲線　；　P = AS （ Y)

と言う関係から、まず、

　　　　ND；w／P =ｄF／ｄN　　　　【実質賃金＝限界生産力】

　　　　NS ; w ／P = ｜ｄH／ｄN ｜　 【実質賃金＝｜限界不効用｜】

であったから、

　　　　ND(w・P ) = NS ( w・P )

となるが、上述、ｗは下方硬直的名目賃金ｗであり、、一定の予見の下に与えられる数字・定数となる事から、結局、

　　　　　　　　N= N ( P｜ｗ ) 【 このNは、労働需要量を表す関数としてのN ]

と表す事でき、更に、

　　　　　　　　Y= F (N )　は、　N= F^ (Y ) から、

　　　　　　　　 N ( P ｜ｗ ) = F^ ( Y )

となり、最終的にAS曲線は、

　　　　　　　　P = AS ( Y ｜ｗ )

と言う式になる。そこで、大分上になるが、AD曲線は

　　　　　 AD; P = AD ( e・Y )

であったので、P-Y平面上ではeを外生変数とすれば、AD・AS曲線が図示し得る事になり,また、

　　　　　　Y = AS^ ( P ｜ｗ ) = AD^ ( p ・e )

　　　　　　　　P = (AD/AS) ( e ｜ｗ )

となり、先のIS-LMｰBP分析上の三式と合わせ

　　　　　IS; Y= IS（ｒ・e｜ｃ・G・X・ｍ）

　　　　　LM；M ＝ LM（ｒ・Y・P )

　　　　　BP; r= BP（e・Y｜X・ｍ・ｋ・r* ) = R

　　　　　AD-AS; P= (AD/AS) (e｜ｗ ・ｃ・G・X・ｍ・M)

と、四つの未知数に対し四本の式が対応し、解を得る事が分かる。即ち、IS-LM-BP分析とAD-AS分析を並行して行いうる（数学的）理論根拠＃を得た事になる。

＃Ⅱｰ5、補遺として、簡便な関数を用いて、AD並びにAS曲線を導出してみたので参照して戴きたい。

従って、二国間AD-AS分析について、少なくとも”小国”の立場の国の分析については、IS-LM-BP分析によりその”至当性”を検証する事が出来る根拠を得たことにもなると考える。

翻って、マンデルｰフレミング・モデルでは、P=一定とするために、簡便に相応の”知見”を得られる（なおかつ、上述、扱いが”面倒”なPを未知数に加えても、得られる”知見”に大差ない、と言うことでもあろう）為に、経済分析において、頻繁に用いられるものと思うが、その知見の一つが、「資本移動が自由な場合においては、為替の変動を通じて、金融緩和は経済拡大に（大いに）効果がある」とするものが、最初の図の左側のIS-LM-BP分析の図であった訳である。

この（狭義の）マンデルｰフレミング・モデルによって得られる他のケース・知見については、ページが長くなったので、次ページ以降で見てみたいと思う。