まず、AS曲線の導出を行う。

 

以上、計算過程が間違ってなければ、生産関数をF(N)=２a√Nと置けば、Yf・Pにつきa・bの関係式として規定し得るから、任意の数字を入れてみると、次の結果が得られる。

 

 

 

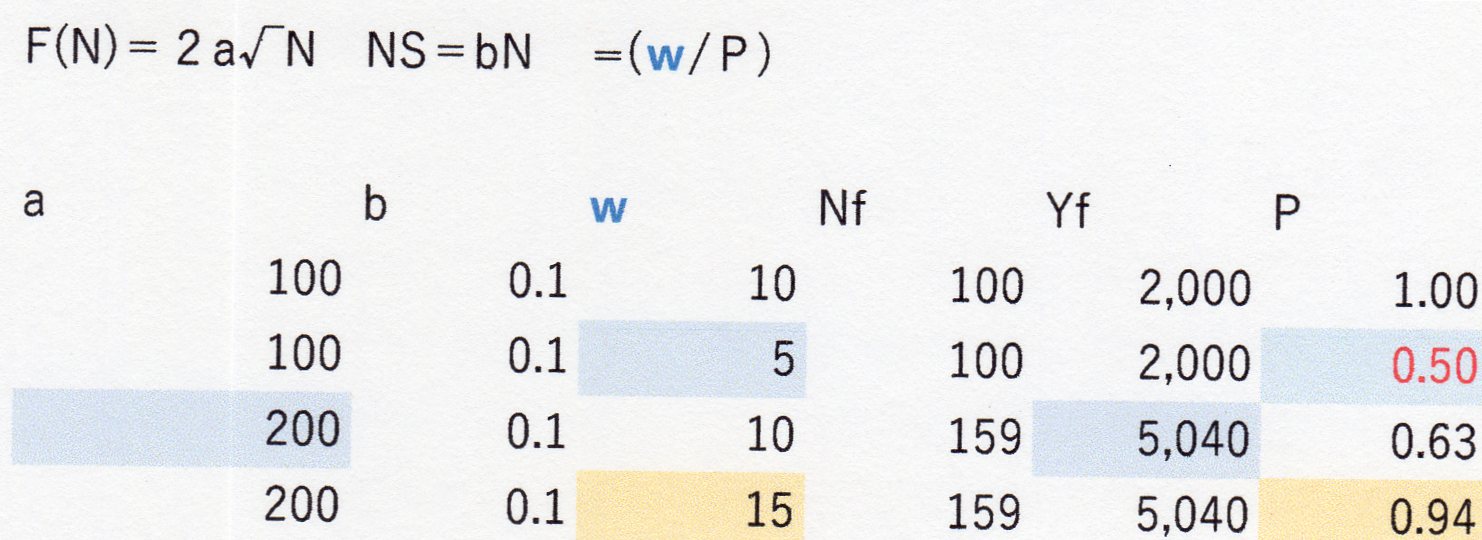
まず,適当にaを100としてｂを0.1、硬直的名目賃金ｗを10として計算してみると、Nf100・Yf2,

000となりPは1.00を得る。（適当とは云え、随分簡便な数値とはなるが）

そこで、ｗを5に低下させてみるとNf・Yfの値は変らず、Pは0.50に下がる。

一方、aを200にしｗは当初の10に戻してみると、Nfは159にYfは5,040に拡大するが、Pは0.63にa=100の時のP=1.00から低下する。

また、この際、P=１に近いP=0.94の時に、ｗは15迄上昇可能である。

これらAS曲線の具体例の結果から、賃金低下または生産性上昇により、AS曲線の下方シフトが生じる事が例証され、また、賃金低下の際のAS曲線の下方シフトは、所得拡大をもたらさないが、生産上昇によるAS曲線の下方シフトは、完全雇用時国民所得の拡大をもたらす事も例証された。

これらの結果をⅡｰ5で示した3連図を若干修正して以下に図示する。

 

 

 

 

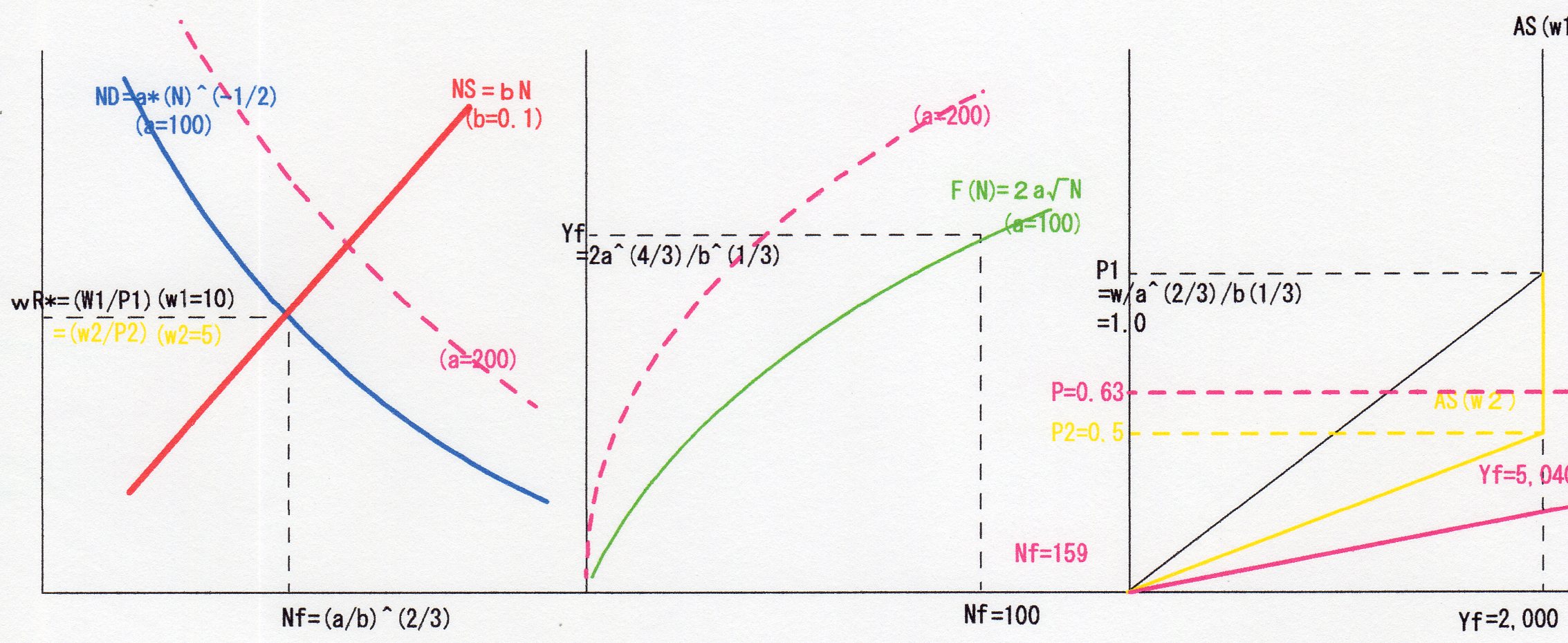
生産関数F(N)は、Ⅱｰ5で示した際も同じ曲線を用いているが√関数は、ｄF/dN（＝ｆ’と置く）＞０だが、ｄｆ’/ｄＮ＜０と、”収穫逓減の法則”をうまく（？）表す為に、よく用いられいる（と理解している）。従って、Ⅱｰ5のＮＤは直線で表していたが、√関数は二次微分が負であることから,上図の如く、原点に凸の曲線となる。

なお、a=200とした生産性上昇の場合のND及びF(N),並びにNf=159は単なる図示であるが、AS曲線の傾きは、P1・Yfの原点からの作図上の距離に基づきJW-CADで作図しており（実際は右方向に垂直部分まで作図してあるが、スキャン・本ページの横幅の関係でカットしてある）、計算数値に対応した本来の傾きである。

 

では、次にAD曲線の導出を行う。

 

 

 

この導出においては、一般（例題）に用いられている一次式をI(r)並びにLM(ｒ・Y)に用いた。

特にLM関数においては生産性分析によく見かけるコブｰダグラス関数乃至セス関数がいいのではと思われるが、計算が複雑になり、そのような計算例も学習したことがなく自信もないので、初等的ではあるが、一応関数的特性は満たす、一次式としている。

結果、AD曲線の式は、Ⅱｰ5で述べたAD(P・Y・e)となる関係を、（P・Y）＝（０・Y#)を原点とする、原点に凸の曲線として示すことが出来た。

これは、古典派の”AD曲線”であるM=ｋ＊P＊Y＊と結果的乃至形状的には変らないが、これは、上述、LM関数をｒ乃至Yの一次式としている為である（と思われる）

ここで、注目されるのは、SFⅡｰ2でBP曲線を導入する際に、内生変数P並びに定数MやX・ｍまた、外生変数たるeの変化によりAD曲線がどうシフトするかのグラフを示す際に右シフトする、なり、左シフトする、と述べていたが、上記式を見ると、確かにM+では上方シフトするが、e+やX+・ｍ＋では曲線がシフトする訳ではなく、Y#がシフトする為に、元の（０・Y#)を原点とすれば、AD曲線自体がシフトしている、と見做されると言うことである。

そこで、Ⅱｰ2で示したグラフを修正して以下に示すことにする。

 

 

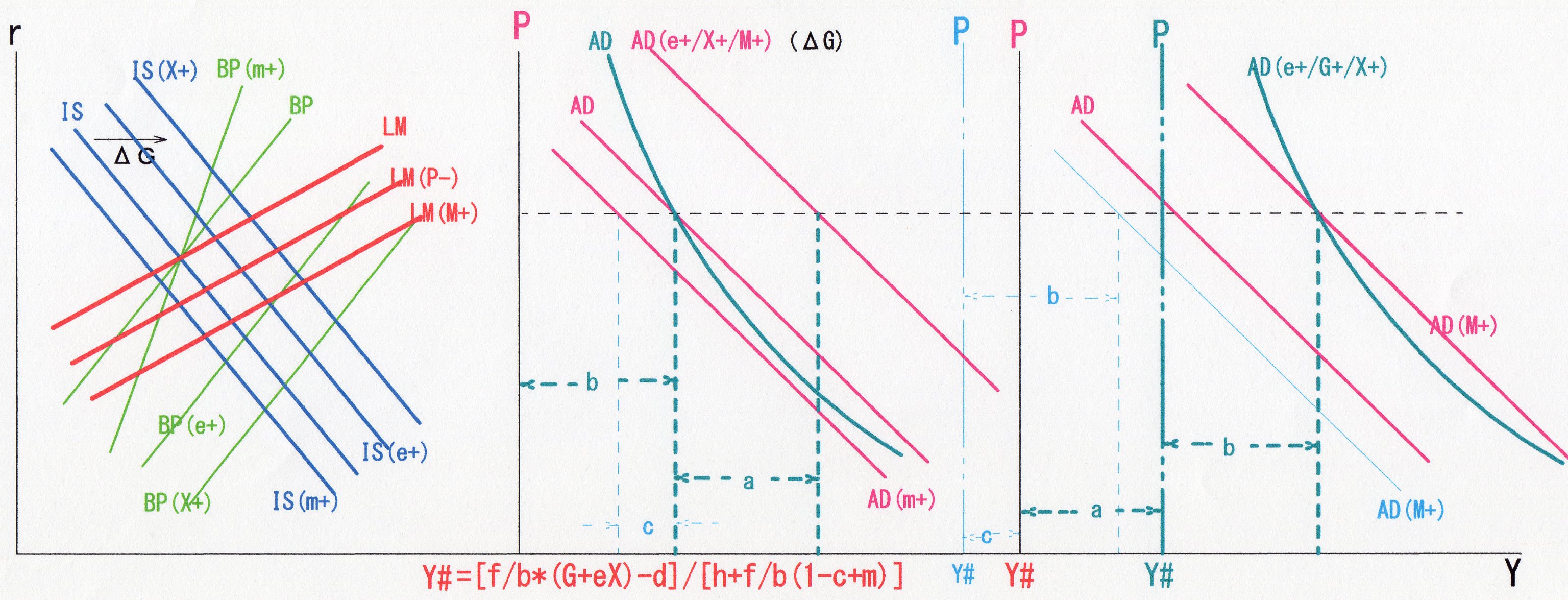
まず、左のIS-LM-BP分析図において、Ⅱｰ2で示した際にはΔGの変化を示していなかったがΔG増加すれば、当然右シフトする。

次に中のAD-AS図において、Ⅱｰ2で示した際はAD曲線は直線ADで表していたが、上記導出された式ではADの曲線と成る。

そこで、LM曲線がMの増加によりLM(M+)へ下方シフトした際は、導出した式から、中の図の通りに、一番右の図においても、AD（M+)に確かに上方シフトする。

しかし、e+・X+・ΔGの増加の場合、導出した式上、Y#がY#にシフトする為に、P-Y#上はシフトするかに見えるがP-Y#上で見れば、変化はしていないことが分かる。

どこででもいいのだが、分かりやすいように中の図で、ADとADの交点を水平に点線で結んであるが、この点線のPｰY#軸との交点とADとADの交点との距離をｂとし、M+同等の変化をe+・X+・ΔGの増加により引き起こすとしてその量をaとすれば、P-Y#軸はP-Y#軸からaの距離を右に移動して,右の図のP-Y#軸となる。

この時、ADの原点（０・Y#）に対する位置関係は変らないから、（P・Y#)＝（０・Y#)からｂの距離で先程の水平の点線上にAD（M+)とAD（e+・G+・X+)の交点が位置している事になる。

これを、PｰY#から見ればAD(M+)同様,AD（e+・G+・X+)も右シフトしていると見做されることになる。

また、ｍ＋によりAD曲線が左シフトする場合については、先ほどのAD-ADの交点から水平の点線上Cの距離を左にシフトする際には、PｰY#軸がP-Y#軸にCだけ左に移動し、AD曲線の原点に対する位置関係は変らないからPｰY#軸に対しｂの距離の垂直線と先の水平の破線の交点にAD(m+)が位置していることになる。そして、先ほど同様P-Y#軸から見れば左にAD曲線がシフトしているように見做されるわけである。（なお、このAD(M+)は、図の煩瑣を避けるために直線のまま示している）

もっとも、P-Y#軸を（P・Y）＝（０・０）を原点として描き切り、（０・０）から全体図を見れば、確かに右乃至左シフトしている訳であり、この観点から”簡便的”にM+以外の場合も軸が移動していると言わずに、グラフが右乃至左シフトしている、と表現し得る事は理解されるが、飽くまで、上述の点を理解していなければと思う。（但し、これは、I(r)等に一次式を用いた結果にしか過ぎないかも知れず、先ほどのコブｰダグラス関数等を用いた場合にどう”表現”されるかは存知しない）